梯度下降法 —— 经典的优化方法
本站寻求有缘人接手，详细了解请联系站长QQ1493399855
梯度下降法 —— 经典的优化方法
机器学习基础算法python代码实现可参考：zlxy9892/ml_code
1 原理
在机器学习的核心内容就是把数据喂给一个人工设计的模型，然后让模型自动的“学习”，从而优化模型自身的各种参数，最终使得在某一组参数下该模型能够最佳的匹配该学习任务。那么这个“学习”的过程就是机器学习算法的关键。梯度下降法就是实现该“学习”过程的一种最常见的方式，尤其是在深度学习(神经网络)模型中，BP反向传播方法的核心就是对每层的权重参数不断使用梯度下降来进行优化。
梯度下降法(gradient descent)是一种常用的一阶(first-order)优化方法，是求解无约束优化问题最简单、最经典的方法之一。我们来考虑一个无约束优化问题
, 其中 
为连续可微函数，如果我们能够构造一个序列 ，并能够满足：
那么我们就能够不断执行该过程即可收敛到局部极小点，可参考下图。
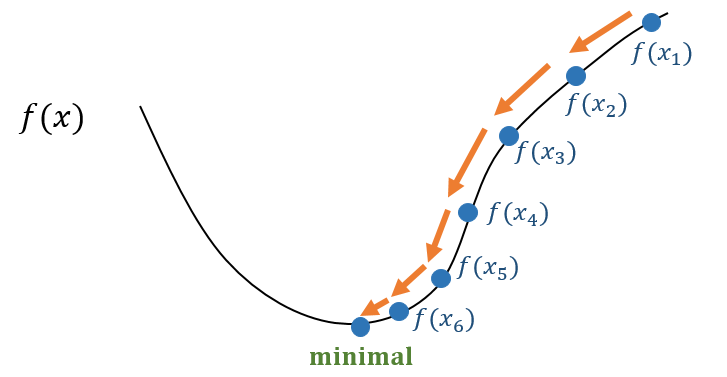
寻找最小点过程
那么问题就是如何找到下一个点 
,并保证 
呢？假设我们当前的函数 的形式是上图的形状，现在我们随机找了一个初始的点 ，对于一元函数来说，函数值只会随着
的变化而变化，那么我们就设计下一个 是从上一个
沿着某一方向走一小步
得到的。此处的关键问题就是：这一小步的方向是朝向哪里？
对于一元函数来说， 是会存在两个方向：要么是正方向( 
)，要么是负方向（ 
），如何选择每一步的方向，就需要用到大名鼎鼎的泰勒公式，先看一下下面这个泰勒展式：
左边就是当前的 移动一小步 
之后的下一个点位，它近似等于右边。前面我们说了关键问题是找到一个方向，使得 ，那么根据上面的泰勒展式，显然我们需要保证：
可选择令：
其中步长 α是一个较小的正数，从而： .
由于任何不为0的数的平方均大于0因此保证了 .
从而，设定：
,则可保证：
那么更新 的计算方式就很简单了，可按如下公式更新
这就是所谓的沿负梯度方向走一小步。
到此为止，这就是梯度下降的全部原理。
如果稍有不清楚的地方，再用下图重新回顾一下具体的设计过程：
梯度下降法的设计过程
2 代码实现
不妨用python来自己尝试一下上述的梯度下降法是否真的能够帮助我们找到函数的极小值点吧。
完整代码：https://github.com/zlxy9892/ml_code/blob/master/basic_algorithm/gradient_descent/simple_gradient_descent.py
# -*- coding: utf-8 -*-import numpy as np
import matplotlib.pyplot as pltdef f(x):return np.power(x, 2)def d_f_1(x):return 2.0 * xdef d_f_2(f, x, delta=1e-4):return (f(x+delta) - f(x-delta)) / (2 * delta)# plot the function
xs = np.arange(-10, 11)
plt.plot(xs, f(xs))
plt.show()learning_rate = 0.1
max_loop = 30x_init = 10.0
x = x_init
lr = 0.1
for i in range(max_loop):# d_f_x = d_f_1(x)d_f_x = d_f_2(f, x)x = x - learning_rate * d_f_xprint(x)print('initial x =', x_init)
print('arg min f(x) of x =', x)
print('f(x) =', f(x))输出内容如下：
8.000000000004661
6.400000000004837
5.120000000003557
4.0960000000043095
3.276800000005622
2.6214400000032967
2.097152000001259
1.6777216000003392
1.3421772800004028
1.0737418240003205
0.8589934592002546
0.6871947673602241
0.5497558138881831
0.4398046511105336
0.35184372088844174
0.2814749767107627
0.22517998136861533
0.18014398509489674
0.14411518807592116
0.11529215046073862
0.09223372036859068
0.07378697629487216
0.05902958103589708
0.047223664828717364
0.03777893186297355
0.03022314549037856
0.024178516392302875
0.019342813113842325
0.015474250491073885
0.012379400392859128
initial x = 10.0
arg min f(x) of x = 0.012379400392859128
f(x) = 0.00015324955408672073经过30次迭代 从初始点10.0逐步逼近最小点 
.